Krahasimi i thyesave

 Meqë thyesat paraqesin pjesë të një tërësie, si të tilla ato mund të krahasohen mes vete.

Dallojmë tri raste:

1. Krahasimi i thyesave me emërues të njëjtë
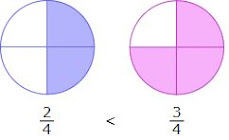
Le të krahasojmë thyesat `\frac 2 4` dhe `\frac 3 4`

Nga figura shohim se thyesa `\frac 3 4` paraqet sasi më të madhe të hijëzuar sesa thyesa `\frac 2 4`, andaj si e tillë është më e madhe.

Tani le të krahasojmë thyesat `\frac 3 8` dhe `\frac 7 8`

Nga figura shohim se thyesa `\frac 7 8` paraqet sasi më të madhe të hijëzuar sesa thyesa `\frac 3 8`, andaj si e tillë është më e madhe.

Pra, në rastin kur dy thyesa kanë të njëjtin emërues atëherë më e madhe do të jetë ajo thyes e cila ka numëruesin më të madh.

2. Krahasimi i thyesave me numërues të njëjtë
Le të krahasojmë thyesat `\frac 1 4` dhe `\frac 1 10`

Nga figura shohim se thyesa `\frac 1 4`  paraqet sasi më të madhe të hijëzuar sesa thyesa `\frac 1 10`, andaj si e tillë është më e madhe.

Tani le të krahasojmë thyesat `\frac 3 4` dhe `\frac 3 5`

Nga figura shohim se thyesa `\frac 3 4`  paraqet sasi më të madhe të hijëzuar sesa thyesa `\frac 3 5`, andaj si e tillë është më e madhe.

Pra, në rastin kur dy thyesa kanë të njëjtin numërues atëhere më e madhe do të jetë ajo thyes e cila ka emëruesin më të vogël.

3. Krahasimi i thyesave me emërues dhe numërues të ndryshëm

Zakonisht për të krahasuar thyesat që nuk kanë as emërues e as numërues të njëjtë përdorim metodën e fluturës, me ç´rast numëruesi i thyesës së parë shumëzohet me emëruesin e thyesës së dytë, ndërsa numëruesi i thyesës së dytë shumëzohet me emëruesin e thyesës së parë.

Le të konsiderojmë rastin e krahasimit të thyesave `\frac 5 6` dhe `\frac 7 8`

Shohim se në anën e majtë kemi fituar numrin 40 nga shumëzimi i numrave 5 dhe 8, ndërsa në anën e djathtë është fituar numri 42 nga shumëzimi i numrave 7 dhe 6. Si dhe dijmë që 40<42 andaj e njëjta shenjë (<) bartet tek thyesat.

Pra, `\frac 5 6` < `\frac 7 8`.

Le të konsiderojmë tani rastin e thyesave  `\frac 4 6` dhe `\frac 3 10`.
Shumëzojmë duke përdorur metodën e fluturës, dhe shohim se në anën e majtë kemi 40 kurse në anën e djathtë 18.

 Meqë 40>18 dhe këtë shenjë (>) e vendosim mes thyesave.

Për të luajtur një lojë ku përdoret krahasimi i thyesave kliko këtu.

Detyrë shtëpie
Krahasoni thyesat e mëposhtme:

a)  `\frac 5 8` dhe `\frac 2 8`

b)  `\frac 4 6` dhe `\frac 4 9`

c)  `\frac 7 9` dhe `\frac 3 4`

d)  `\frac 3 6` dhe `\frac 4 8`